C Binary Tree with an Example C Code (Search, Delete, Insert Nodes)

by Himanshu Arora on February 27, 2013

Binary tree is the data structure to maintain data into memory of program. There exists many data structures, but they are chosen for usage on the basis of time consumed in insert/search/delete operations performed on data structures.

Binary tree is one of the data structures that are efficient in insertion and searching operations. Binary tree works on O (logN) for insert/search/delete operations.

Binary tree is basically tree in which each node can have two child nodes and each child node can itself be a small binary tree. To understand it, below is the example figure of binary tree.

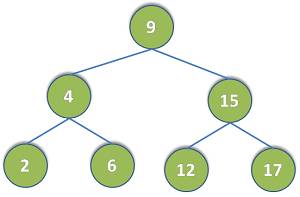
Binary tree works on the rule that child nodes which are lesser than root node keep on the left side and child nodes which are greater than root node keep on the right side. Same rule is followed in child nodes as well that are itself sub-trees. Like in above figure, nodes (2, 4, 6) are on left side of root node (9) and nodes (12, 15, 17) are on right side of root node (9).

We will understand binary tree through its operations. We will cover following operations.

Create binary tree
Search into binary tree
Delete binary tree
Displaying binary tree

Creation of binary tree

Binary tree is created by inserting root node and its child nodes. We will use a C programming language for all the examples. Below is the code snippet for insert function. It will insert nodes.

11 void insert(node ** tree, int val) {
12 node *temp = NULL;
13 if(!(*tree)) {
14   temp = (node *)malloc(sizeof(node));
15   temp->left = temp->right = NULL;
16   temp->data = val;
17   *tree = temp;
18   return;
19 }
20
21 if(val < (*tree)->data) {
22      insert(&(*tree)->left, val);
23   } else if(val > (*tree)->data) {
24     insert(&(*tree)->right, val);
25   }
26 }

This function would determine the position as per value of node to be added and new node would be added into binary tree. Function is explained in steps below and code snippet lines are mapped to explanation steps given below.

[Lines 13-19] Check first if tree is empty, then insert node as root.

[Line 21] Check if node value to be inserted is lesser than root node value, then

a. [Line 22] Call insert() function recursively while there is non-NULL left node
b. [Lines 13-19] When reached to leftmost node as NULL, insert new node.

[Line 23] Check if node value to be inserted is greater than root node value, then

a. [Line 24] Call insert() function recursively while there is non-NULL right node
b. [Lines 13-19] When reached to rightmost node as NULL, insert new node.

Searching into binary tree

Searching is done as per value of node to be searched whether it is root node or it lies in left or right sub-tree. Below is the code snippet for search function. It will search node into binary tree.

46 node* search(node ** tree, int val) {
47 if(!(*tree)) {
48   return NULL;
49  }
50 if(val == (*tree)->data) {
51   return *tree;
52  } else if(val < (*tree)->data) {
53    search(&((*tree)->left), val);
54  } else if(val > (*tree)->data){
55    search(&((*tree)->right), val);
56  }
57 }

This search function would search for value of node whether node of same value already exists in binary tree or not. If it is found, then searched node is returned otherwise NULL (i.e. no node) is returned. Function is explained in steps below and code snippet lines are mapped to explanation steps given below.

[Lines 47-49] Check first if tree is empty, then return NULL.
[Lines 50-51] Check if node value to be searched is equal to root node value, then return node
[Lines 52-53] Check if node value to be searched is lesser than root node value, then call search() function recursively with left node
[Lines 54-55] Check if node value to be searched is greater than root node value, then call search() function recursively with right node
Repeat step 2, 3, 4 for each recursion call of this search function until node to be searched is found.

Deletion of binary tree

Binary tree is deleted by removing its child nodes and root node. Below is the code snippet for deletion of binary tree.

38 void deltree(node * tree) {
39 if (tree) {
40   deltree(tree->left);
41   deltree(tree->right);
42   free(tree);
43  }
44 }

This function would delete all nodes of binary tree in the manner – left node, right node and root node. Function is explained in steps below and code snippet lines are mapped to explanation steps given below.

[Line 39] Check first if root node is non-NULL, then

a. [Line 40] Call deltree() function recursively while there is non-NULL left node
b. [Line 41] Call deltree() function recursively while there is non-NULL right node
c. [Line 42] Delete the node.

Displaying binary tree

Binary tree can be displayed in three forms – pre-order, in-order and post-order.

Pre-order displays root node, left node and then right node.
In-order displays left node, root node and then right node.
Post-order displays left node, right node and then root node.

Below is the code snippet for display of binary tree.

28 void print_preorder(node * tree) {
29 if (tree) {
30 printf("%d\n",tree->data);
31 print_preorder(tree->left);
32 print_preorder(tree->right);
33 }
34 }
35 void print_inorder(node * tree) {
36 if (tree) {
37 print_inorder(tree->left);
38 printf("%d\n",tree->data);
39 print_inorder(tree->right);
40 }
41 }
42 void print_postorder(node * tree) {
43 if (tree) {
44 print_postorder(tree->left);
45 print_postorder(tree->right);
46 printf("%d\n",tree->data);
47 }
48 }

These functions would display binary tree in pre-order, in-order and post-order respectively. Function is explained in steps below and code snippet lines are mapped to explanation steps given below.

Pre-order display

a. [Line 30] Display value of root node.
b. [Line 31] Call print_preorder() function recursively while there is non-NULL left node
c. [Line 32] Call print_preorder() function recursively while there is non-NULL right node

In-order display

a. [Line 37]Call print_inorder() function recursively while there is non-NULL left node
b. [Line38] Display value of root node.
c. [Line 39] Call print_inorder() function recursively while there is non-NULL right node

Post-order display

a. [Line 44] Call print_postorder() function recursively while there is non-NULL left node
b. [Line 45] Call print_postorder() function recursively while there is non-NULL right node
c. [Line46] Display value of root node.

Working program

It is noted that above code snippets are parts of below C program. This below program would be working basic program for binary tree.

#include<stdlib.h>
#include<stdio.h>

struct bin_tree {
int data;
struct bin_tree * right, * left;
};
typedef struct bin_tree node;

void insert(node ** tree, int val)
{
    node *temp = NULL;
    if(!(*tree))
    {
        temp = (node *)malloc(sizeof(node));
        temp->left = temp->right = NULL;
        temp->data = val;
        *tree = temp;
        return;
    }

    if(val < (*tree)->data)
    {
        insert(&(*tree)->left, val);
    }
    else if(val > (*tree)->data)
    {
        insert(&(*tree)->right, val);
    }

}

void print_preorder(node * tree)
{
    if (tree)
    {
        printf("%d\n",tree->data);
        print_preorder(tree->left);
        print_preorder(tree->right);
    }

}

void print_inorder(node * tree)
{
    if (tree)
    {
        print_inorder(tree->left);
        printf("%d\n",tree->data);
        print_inorder(tree->right);
    }
}

void print_postorder(node * tree)
{
    if (tree)
    {
        print_postorder(tree->left);
        print_postorder(tree->right);
        printf("%d\n",tree->data);
    }
}

void deltree(node * tree)
{
    if (tree)
    {
        deltree(tree->left);
        deltree(tree->right);
        free(tree);
    }
}

node* search(node ** tree, int val)
{
    if(!(*tree))
    {
        return NULL;
    }

    if(val < (*tree)->data)
    {
        search(&((*tree)->left), val);
    }
    else if(val > (*tree)->data)
    {
        search(&((*tree)->right), val);
    }
    else if(val == (*tree)->data)
    {
        return *tree;
    }
}

void main()
{
    node *root;
    node *tmp;
    //int i;

    root = NULL;
    /* Inserting nodes into tree */
    insert(&root, 9);
    insert(&root, 4);
    insert(&root, 15);
    insert(&root, 6);
    insert(&root, 12);
    insert(&root, 17);
    insert(&root, 2);

    /* Printing nodes of tree */
    printf("Pre Order Display\n");
    print_preorder(root);

    printf("In Order Display\n");
    print_inorder(root);

    printf("Post Order Display\n");
    print_postorder(root);

    /* Search node into tree */
    tmp = search(&root, 4);
    if (tmp)
    {
        printf("Searched node=%d\n", tmp->data);
    }
    else
    {
        printf("Data Not found in tree.\n");
    }

    /* Deleting all nodes of tree */
    deltree(root);
}

Output of Program:

It is noted that binary tree figure used at top of article can be referred to under output of program and display of binary tree in pre-order, in-order and post-order forms.

$ ./a.out
Pre Order Display
9
4
2
6
15
12
17
In Order Display
2
4
6
9
12
15
17
Post Order Display
2
6
4
12
17
15
9
Searched node=4

Add your comment

If you enjoyed this article, you might also like..

Tagged as: Binary Tree Deletion, Binary Tree in C, Binary Tree Remove, Binary Tree Remove Node, Binary Tree Search C Code, C Binary Tree Insert, C Binary Tree Search, Display Binary Tree, Optimal Binary Search Tree

Comments on this entry are closed.

Bob February 27, 2013, 9:45 am

Cool. Thanks for the explanation.
With C++ STL Libraries, we don’t have to write this but it is good to know basics.
If you have time, it may be a good idea of going thru the C++ STL libraries and give example code to do this as well as others (e.g. maps, vectors) to show to use them

∞
marcio February 27, 2013, 10:18 am

When you say O (log N): N is the number of nodes or the height of the tree?

∞
bhupesh February 27, 2013, 12:36 pm

nice explanation. But binary tree doesn’t have any rule regarding the key value of a node. It’s binary search tree.

∞
Gaurang S February 27, 2013, 1:41 pm

Hello,

Good article!
1. I think the explanation and algorithms mentioned are of a Binary search tree (BST)
2. Also for a Binary search tree worst case insert/delete/search would be O(N), where N is the number of elements. The worst case for insertion would occur when the elements are in ascending or descending order in which nodes will keep on appending to right or to left respectively.

∞
Georgi K March 1, 2013, 2:22 am

It is nice to have a simple C implementation — a lot of embedded micros have no C++ at all, neither STL.
For me search() didn’t find the ‘4’ element, so I added this one:
node* search2(node * tree, int val) {
if( ! tree ) return NULL;
if(val data) {
return search2(tree->left, val);
} else if(val > tree->data) {
return search2(tree->right, val);
}
return tree;
}

∞
DuskoKoscica March 4, 2013, 2:43 am

It is nice, but in some case binary tree is not good enough, and yes you can use the hip.
But, what I would like to read about, is the tree that can have many sub trees..
Like multy way tree..
That would be nice article…

∞
Robert Nix March 27, 2013, 1:07 pm

A function missing from your program and description is balancing the binary tree…

Given your implementation, the worst possible data you could feed the program would be a pre-sorted list, because all the values would cascade down the right side of the tree, never using the left nodes at all. This, effectively, would simply be a linked list, with a lot of non-useful compares of the left node addresses.

Adding a tree balancing routine to be called after insertions would solve this problem.

∞
Payal April 7, 2013, 4:46 am

search isn’t working:(

∞
Joe May 6, 2013, 5:36 pm

Can you point me in the direction to applying this to strings instead of integers? Saying building a tree with H,G,A, etc…

∞
Robert Nix May 7, 2013, 6:45 pm

Since it’s just a comparison, the code should work equally well for numbers or letters. Just change the variable type used.

∞
DuskoKoscica May 8, 2013, 7:08 am

Now it might sound funny, but if you wanna combine the char and int or float, and some other things you could use unions, and struct, and so on…

∞
wisnusakti May 27, 2013, 6:46 pm

tank’s. but function search isn’t working, and in function insert “temp” that never used

∞
debbie xu June 19, 2013, 12:26 pm

“tmp = search(&root, 4);” could be “tmp = search(root,4)”, of course you need to change the prototype of search into “node* search(node * tree, int val)” and implementation inside accordingly.

Either way, I also ran into problem with search: actually the code found the searched node, it’s just that the simple assignment of “tmp=xxx” doesn’t work. I printed out the value returned from search() before it returns, and the tmp after it has been assigned to the search() result, they don’t match !!! can’t figure out why. so I added a third parameter into search() to get the result as following:

node* search(node * tree, int val, node **found)
{
*found = NULL;

if(!(tree))
{
return NULL;
}

if(val data)
{
search(((tree)->left), val, found);
}
else if(val > (tree)->data)
{
search(((tree)->right), val, found);
}
else if(val == (tree)->data)
{
*found = tree;
return tree;
}
}

and call it in main like this:

tmp1 = search(root, 15, &tmp2);

Now tmp2 points to the right node, but tmp1 points to some garbage.

Anybody can figure out why the original search() result can’t be assigned correctly? I used gcc on Linux 2.6.25.

∞
debbie June 19, 2013, 1:15 pm

figured it out, the recursive call didn’t return the value. should be like this:

if(val data)
{
return search(((tree)->left), val, found);
}
else if(val > (tree)->data)
{
return search(((tree)->right), val, found);
}

and forget about adding a third parameter into search, no need for it.

∞
Habib Beidoun September 26, 2013, 2:48 am

Fix the search function by adding “return” in front of the two recursive search calls, e.g.,
return search(&((*tree)->left), val);

The function search does not really require a pointer to a pointer in the first argument (a pointer would suffice), as that value is not used by the caller and there is already a return.

∞
Andrew November 2, 2013, 12:06 pm

Hi. It’s a good explanation of BST. But I have a question about your deltree function.
C language is the language where function parameters are always passed by value.
In this function you pass root pointer as node *root. How free()-function can delete its value and free a memory?

∞
M.Z.M.Hanafy January 30, 2014, 12:16 am

Thank you so much. Its really excellent work.

∞
arul April 15, 2014, 7:54 am

awesome examples

∞
Raghu April 28, 2014, 3:16 am

Hi.. I just have clarification… Please some one help me…
When calling insert function what is the need to pass root it with ‘&’ rather than just root and De-refrenecing it **?

We can achieve it by passing just root and with single * De-referencing?.

∞
NB.Gowri July 31, 2014, 8:11 am

but tis is program for binary search tree not binary tree.plz anybody post the code for binary tree.

∞
Nirav August 6, 2014, 9:40 am

This is Binary Search Tree, not Binary Tree.

∞
srinadh November 5, 2014, 10:39 pm

delete function not working properly

∞
Anupam November 6, 2014, 10:58 am

void deltree(node * tree) should take pointer to pointer i.e void deltree(node ** tree)

∞
Mohit Awasthi November 15, 2014, 7:44 am

Hello!! I want some help.
I am trying to write a program to delete an item from a binary search tree.
I succeeded but I found some problem when I tried to delete the root item, so if anyone can help me I will be very grateful.

Thanks in advance.

∞
prakash May 17, 2015, 8:45 am

What a fantastic explanation.thanks

∞
chetan khatal October 23, 2015, 2:27 am

this programe output is automatic but how to do run by user

∞
Vipin December 30, 2015, 8:51 am

This is not binary tree , it is binary search tree.

Binary tree: Tree where each node has up to two leaves

1
/ \
2 3

Binary search tree: Used for searching. A binary tree where the left child contains only nodes with values less than the parent node, and where the right child only contains nodes with values greater than or equal to the parent.

2
/ \
1 3

∞
João Antônio Cardoso March 14, 2016, 4:09 pm

Gcc warns about the search function because it reaches its end without return anything so I fixed it with following:

node_t* search(node_t *tree, int i)
{
if(!tree) return NULL;
else if(i == (*tree).data) return tree;
else if(i < (*tree).data) return search((*tree).left, i);
else return search((*tree).right, i);
}

∞
r.veera reddy May 20, 2016, 8:33 pm

contents regarding data structures is very good

∞

yipkit June 1, 2016, 5:17 am

node delet(ElementType x, node t)
{
	node temp;
	
	if(t==NULL)
		printf("\n Element not found");
	else
	{
		if(xelement)
			t->left=delet(x,t->left);
		else if(x> t->element)
			t->right=delet(x,t->right);
		else
		{
			if(t->left && t->right)
			{
				temp=findmin(t->right);
				t->element=temp->element;
				t->right=delet(t->element,t->right);
			}
			else if(t->left==NULL)
			{
				temp=t;
				t=t->right;
				free(temp);
			}
			else
			{
			temp=t;
			t=t->left;
			free(temp);
			}
		}
	}
	return t;
}

I am sorry, this function can’t run. How to correct this function?

∞

Ubaid Rasheed March 17, 2017, 1:40 pm

thank u so much i am clear now thank u so much

∞
janani April 13, 2017, 10:45 pm

I hate u c program

∞

timnixon April 24, 2017, 7:15 am

Search does not need to take a pointer to a pointer since it does not modify the tree. It just adds complexity.

node* search(node * tree, int val)
{
    if(!tree)
    {
        return NULL;
    }

    if(val data)
    {
        search(tree->left, val);
    }
    else if(val > tree->data)
    {
        search(tree->right, val);
    }
    else if(val == tree->data)
    {
        return tree;
    }
}

call it like this
tmp = search(root, 4);

∞

aadil May 25, 2017, 11:59 pm

what is wrong with this ??

void insert(int key, Node root) {
		if (root == null) {
			root = new Node(key);
		} else {
			if (key > root.val) {
				insert(key, root.right);
			}
			if (key < root.val) {
				insert(key, root.left);
			}
		}
	}

∞

Next post: How to Copy Files in Linux and Unix? 10 cp Command Examples

Previous post: Linux Sticky Bit Concept Explained with Examples